
|
<- User-Mode Linux - Indice Generale - Copertina - Una risposta a Nikolai Bezroukov -> |

|
Sistemi Liberi
L'articolo...L'articolo è il seguito dell'articolo pubblicato sul numero 43 del PLUTO Journal. |
Nella Parte I di questo articolo abbiamo effettuato una discussione di carattere generale sul software scientifico, lo abbiamo classificato in base a due diversi criteri e abbiamo descritto le più importanti aree applicative. Attingendo alle due classificazioni proposte, procederemo di seguito a vedere alcuni programmi particolarmente interessanti e che possiamo considerare esemplificativi di alcune delle categorie enumerate. Non è mia intenzione essere esaustivo ma intendo solo mostrare, con l'aiuto di alcuni esempi, le loro potenzialità. Durante la discussione saranno forniti i riferimenti per eventuali approfondimenti.
La GNU Scientific Library (http://www.gnu.org/software/gsl/) è una libreria di funzioni molto potente che contiene routine per la computazione numerica nelle seguenti aree:
| Numeri complessi | Radici di polinomi |
| Funzione speciali | Vettori e matrici |
| Permutazioni | Combinazioni |
| Ordinamento | Supporto BLAS |
| Algebra lineare | CBLAS |
| Fast Fourier Transform | Eigensistemi |
| Numeri random | Quadratura |
| Distribuzioni random | Sequenze quasi-random |
| Istogrammi | Statistica |
| Integrazione di Monte Carlo | N-tuple |
| Equazioni differenziali | Simulated annealing |
| Differenziazione numerica | Interpolazione |
| Serie | Approssimazioni di Chebyshev |
| Ricerca di radici | Trasformate discrete di Hankel |
| Fitting per minimi quadrati | Minimizzazione |
| IEEE virgola mobile | Costanti fisiche |
La libreria è diretta ai programmatori C e C++. Essa è stata scritta a sua volta in C e presenta una moderna API che permette la scrittura di programmi per linguaggi di alto livello. Si rimanda alla documentazione riportata in bibliografia [3] per gli approfondimenti.
netlib (http://www.netlib.org/) non è né una libreria né un programma, ma piuttosto un repository, cioè una raccolta di librerie, funzioni e software scientifico in generale, ordinato per categorie. Molto del codice presente in netlib è scritto in FORTRAN. Ogni software contiene tutto il necessario per studiarlo approfonditamente: codice (a volte anche binari per diverse piattaforme), documentazioni, articoli, ecc. Un punto di riferimento obbligato per chi lavora con il software scientifico, che sia o meno un programmatore.
Molti dei programmi inseriti in netlib non hanno una licenza, per cui le condizioni per il loro in alcuni casi sono dubbie. Si può considerare in linea di principio una raccolta di software libero o di software di pubblico dominio, anche se è opportuno documentarsi adeguatamente volta per volta.
Alcune delle librerie e software presenti in netlib sono di così alta qualità che sono diventati punti di riferimento per alcuni tipi di problemi. Librerie come LAPACK, CLAPACK, BLAS e SLATEC sono usate da molti programmi e rappresentano lo stato dell'arte più avanzato in assoluto all'interno dei rispettivi ambiti applicativi.
Per ultimo, netlib fornisce la possibilità di ricerca degli algoritmi secondo la loro codifica GAMS (http://gams.nist.gov/).
pvm (http://www.netlib.org/pvm3/) è una delle librerie contenute nel repository netlib. pvm [4] e permette lo sviluppo di applicazioni di calcolo parallelo, cioè di programmi che lavorano simultaneamente su più processori situati su macchine diverse che complessivamente, nel gergo di pvm, vengono chiamati macchina virtuale. Le caratteristiche principali di pvm3 (versione 3) sono le seguenti:
I nodi fanno girare un demone (pvmd) che si incarica di rimanere in ascolto e processare le chiamate ricevute da altri nodi e di inviare i messaggi. Le applicazioni, naturalmente, devono essere predisposte per la computazione parallela; cioè, dobbiamo essere noi a dire al programma in quale modo e ordine devono essere realizzati i calcoli parziali, e poi in quale modo viene computato il risultato finale a partire da essi. pvm ci consente di evitare tutto il lavoro di sviluppo per l'invio e ricezione dei messaggi, salvando gli aspetti hardware e implementando i meccanismi di sicurezza necessari in questi casi.
openmosix (http://openmosix.sourceforge.net) [1] è un software utilizzato anch'esso per il calcolo parallelo, ma si differenzia notevolmente di software del tipo pvm. openmosix è in realtà un insieme di estensioni kernel; in pratica, una patch applicata al kernel che aggiunge le capacità per la migrazione di processi tra diversi computer collegati via rete, consentendo anche la convivenza di hardware eterogeneo all'interno della rete di calcolo.
Un processo lanciato su qualunque nodo viene fatto migrare dal kernel della macchina su altri nodi in modo da bilanciare al meglio le risorse complessive della rete. Questa ottimizzazione delle risorse può essere centrata sulla velocità dei processori o sulla memoria, consentendo un bilanciamento dei cicli di CPU nel primo caso e della RAM complessiva nel secondo.
I vantaggi e gli svantaggi di openmosix sono legati alla sua natura kernel. Da una parte consente un'integrazione perfetta con il sistema, ma da un'altra non è possibile il controllo da parte dei singoli utenti. Una versione recente (openmosix User Mode) implementa il software in user space, permettendo il controllo da parte degli utenti come per un programma ordinario.
È importante capire la differenza tra openmosix (e altri software per l'ottimizzazione e bilanciamento delle risorse di un insieme di macchine, come condor) e pvm. Quest'ultimo permette la suddivisione di un singolo job tra n processori, per cui i tempi di calcolo vengono diminuiti di 1/n rispetto al calcolo su singolo processore, ma richiede lo sviluppo dell'applicazione appositamente per la suddivisione dei compiti, il recupero dei calcoli parziali e la generazione di quello finale a partire da essi. openmosix, invece, non ha come scopo l'esecuzione più veloce possibile di un singolo job, ma l'esecuzione ottima (che corrisponde all'esecuzione più veloce per un bilanciamento dei cicli di CPU) di un insieme di job. Approssimativamente, possiamo considerare che per openmosix la più piccola unità elaborativa è il processo (alcuni processi eseguiti in modalità multithread possono in realtà essere distribuiti da openmosix su più processori) e questo non può essere distribuito tra l'insieme di CPU per velocizzare l'esecuzione; invece, il lancio di un job su una macchina che sta già lavorando provoca la migrazione di uno dei due processi su un'altra CPU, in modo da massimizzare il numero di cicli di processore eseguiti complessivamente in un dato arco temporale.
bc (http://www.gnu.org/software/bc/) [7] è un linguaggio che supporta operazioni con numeri a precisione arbitraria con esecuzione interattiva di istruzioni. La sintassi è simile al C. Dispone anche di una libreria matematica standard (richiamabile dalla riga di comando con il flag -l). Questo programma può essere considerato un programma di utilità, e la sua principale capacità consiste nel poter realizzare operazioni con una precisione non limitata dalle caratteristiche dell'hardware, cioè possono essere generati e manipolati numeri che occupano più di una parola di memoria.
Un esempio. Ci facciamo stampare i primi cento decimali del numero e (e1, e(1) nella sintassi di bc), la base dei logaritmi naturali:
$ bc -l scale=100 e(1) 2.718281828459045235360287471352662497757247093699959574966967627724\ 0766303535475945713821785251664274 |
units (http://freshmeat.net/projects/units/) è un tipico programma di utilità. Il programma realizza la conversione tra unità di misura diverse. Ad esempio, per convertire libbre a grammi:
$ units
2083 units, 71 prefixes, 32 nonlinear units
You have: lb
You want: g
* 453.59237
/ 0.0022046226 |
units ci informa del numero di unità e prefissi che può usare per le conversioni. Il risultato viene fornito in due modi, che corrispondono alla conversione diretta richiesta e a quella inversa. Così, per passare da libbre a grammi, bisogna moltiplicare per 453.59237, mentre per passare da grammi a libbre bisogna moltiplicare per 0.0022046226 (l'inverso del primo numero dato). Naturalmente, possiamo usare numeri diversi dall'unità:
You have: 3.32 lb
You want: g
* 1505.9267
/ 0.00066404296 |
Questo tipo di utilizzo, la conversione tra unità pure, ha una utilità limitata. Ma quando si cominciano ad avere delle unità composte, la cosa diventa un po' più complessa. Un esempio: il passaggio delle unità di calore specifico dal sistema inglese al Sistema Internazionale:
You have: btu/lb ^F
You want: J/g K
* 4.1868
/ 0.2388459 |
Ci pensa il programma a realizzare tutte le operazione intermedie e, quello che è più importante, a controllare la consistenza dimensionale dell'operazione. Se l'analisi dimensionale non torna, units ce lo fa sapere:
You have: btu/lb ^F
You want: J/g
conformability error
4186.8 m^2 / K s^2
1000 m^2 / s^2 |
Il programma fa altre cose. Ad esempio, lasciando vuoto You want, ci fornisce la definizione di quanto inserito in You have:
You have: gpm You want: Definition: gal/min = 6.3090196e-05 m^3 / s |
Inoltre, può funzionare anche come calcolatrice:
You have: pi*2 You want: Definition: 6.2831853 |
Per ultimo, il programma può lavorare con i simboli delle costanti fisiche più importanti, tra le quali ci sono:
| pi | numero π |
| c | velocità della luce nel vuoto |
| e | carica dell'elettrone |
| force | accelerazione della gravità |
| mole | numero di Avogadro |
| water | pressione per altezza unitaria d'acqua |
| Hg | pressione per altezza unitaria di mercurio |
| au | unità astronomica |
| k | costante di Boltzman |
| mu0 | permeabilità del vuoto |
| epsilon0 | permissività del vuoto |
| G | costante gravitazionale |
| mach | velocità del suono |
Contiene anche le masse atomiche di tutti gli elementi chimici:
You have: oxygen You want: Definition: 15.9994 |
units è un programma completo, riuscendo persino a realizzare conversioni non lineari tra unità (quelle che non possono essere trasformate l'una nell'altra applicando un fattore moltiplicativo), come le conversioni tra ^F e ^C. In questi casi queste conversioni possono essere implementate attraverso una ben definita notazione funzionale che però non tratteremo in questa sede. In modo analogo, possono essere inseriti nel database definizioni per nuove unità o trasformazioni tra unità.
gnuplot (http://www.gnuplot.info/) è probabilmente il più noto tra i programmi di rappresentazione funzionale. È anche uno dei più potenti, a mio avviso, dato che permette sia un uso interattivo che non interattivo, per cui può essere usato sia per la creazione di grafici scientifici nelle normali sessioni di lavoro che all'interno di script che devono generare immagini. Inoltre, è ben supportato per l'interfacciamento con altri applicativi, come ad esempio latex [5].
La versione 4 [10] è stata notevolmente potenziata, permettendo l'uso di gradazioni di colore all'interno di grafici di superfici 3D. Si rimanda alla documentazione in bibliografia [6, 9, 10] per ulteriori informazioni.
octave (http://www.octave.org/) [2] può essere considerato l'equivalente per quanto riguarda il software libero del programma mathlab. Questo programma, per chi non lo conoscesse, è un software proprietario molto potente che è diventato uno standard in ambito scientifico. Come mathlab, octave è un programma orientato al calcolo numerico ed è in particolare "specializzato", possiamo dire, nelle manipolazioni matriciali, ma è compatibile con il formato .m nativo di mathlab. Tra quelli che ho visto io, è il programma più versatile per quanto riguarda calcoli che coinvolgono vettori o matrici. Inoltre, è estendibile, per cui è possibile costruire script che usano le funzioni interne o che definiscono nuove funzioni.
octave contiene funzioni predefinite per risolvere problemi nelle seguenti aree:
| Rappresentazione grafica | Ottimizzazione |
| Calcolo matriciale | Statistica |
| Aritmetica complessa | Calcolo con polinomi |
| Funzioni speciali | Control theory |
| Algebra lineare | Processamento di segnali |
| Equazioni non lineari | Processamento di immagini |
| Integrazione | Processamento audio |
| Equazioni differenziali |
Vediamo un esempio: il prodotto di una matrice A di ordine m x
n per una matrice B di ordine n x p per dare come risultato
una matrice m x p:
octave:1> A = rand(2, 3) a = 0.86905 0.54406 0.23879 0.49870 0.61944 0.92069 octave:2> B = rand(3, 5) b = 0.390949 0.313300 0.939757 0.112280 0.088696 0.132804 0.474999 0.933004 0.599052 0.623888 0.121930 0.135812 0.582393 0.065097 0.742529 octave:3> A * B ans = 0.44112 0.56313 1.46337 0.43904 0.59382 0.38949 0.57552 1.58281 0.48701 1.11434 |
dove la funzione rand() serve a creare una matrice di numeri random.
octave può risolvere numericamente equazioni differenziali. Prendiamo, a modo di esempio, il seguente sistema di equazioni differenziali ordinarie:
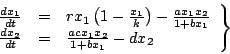
dove le costanti hanno i valori: r = 0.25, k = 1.4, a = 1.5, b = 0.16, c = 0.9, d = 0.8, e le condizioni iniziali sono: x1(0) = 1, x2(0) = 2. L'input dato al programma è il seguente:
octave:1> function xdot = f(x, t)
>
> r = 0.25;
> k = 1.4;
> a = 1.5;
> b = 0.16;
> c = .9;
> d = .8;
>
> xdot(1) = r * x(1) * (1 - x(1) / k) - a * x(1) * x(2) / (1 + b * x(1));
> xdot(2) = a * c * x(1) * x(2) / (1 + b * x(1)) - d * x(2);
>
> endfunction
octave:2> x0 = [1 2];
octave:3> t = linspace(0, 50, 200);
octave:4> y = lsode("f", x0, t);
octave:5> plot(t, y)
octave:6> gset term postscript color solid
octave:7> gset output 'eq_diff.ps'
octave:8> replot |
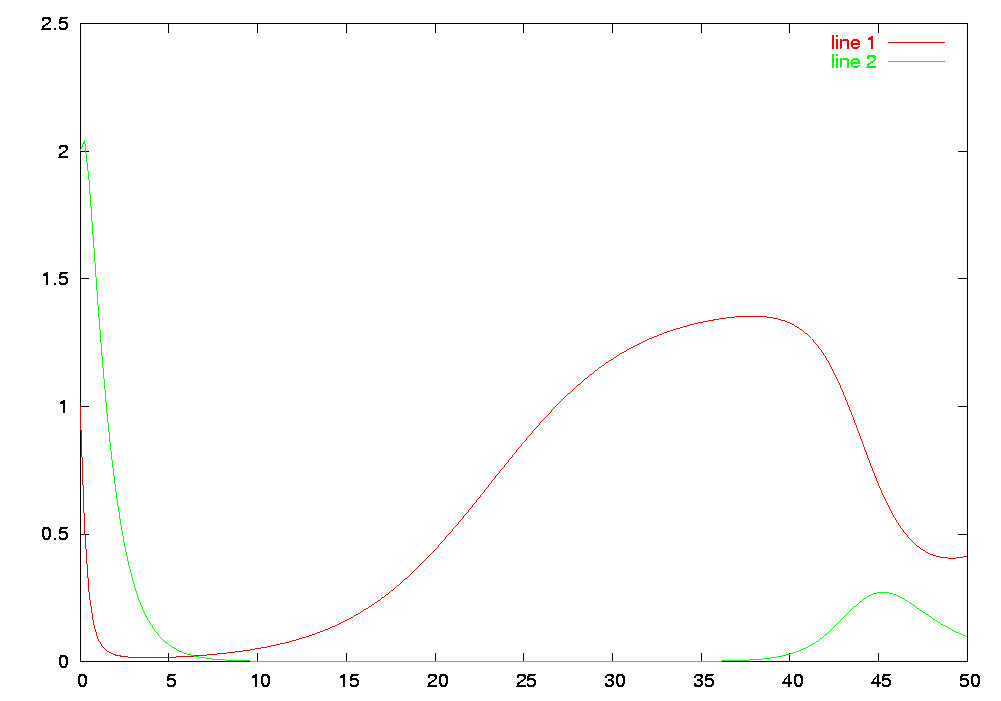
La rappresentazione grafica delle soluzioni è data in figura sottostante, dove si mostra l'andamento delle funzioni x1 e x2 con il tempo t tra t = 0 e t = 50. Questo esempio è buono perché fa vedere come si fa a costruire una funzione per octave. Vediamo brevemente il significato dei comandi.
In primo luogo viene definita la funzione f, che specifica la forma funzionale delle derivate delle funzioni incognite, x1 e x2, rispetto allo scalare t, che è la variabile indipendente (il valore delle derivate è restituita nel vettore xdot). Poi vengono definite le condizioni iniziali, cioè i valori di x1 e x2 a t = 0. linspace restituisce un vettore di, nel nostro caso, 200 valori ugualmente spaziati compresi tra 0 e 50. Per ultimo, lsode realizza l'integrazione del sistema di equazioni rispetto alla variabile indipendente t e tenendo conto delle condizioni iniziali, risultato immagazzinato nella variabile y che viene usato poi dalla funzione plot per la rappresentazione grafica. Il punto e virgola finale istruisce il programma a non fornire in output il risultato delle elaborazioni, ma è possibile visualizzare il risultato dell'integrazione (i valori tabulati di x1 e x2 per i valori specificati di t) inserendo y = lsode("f", x0, t) senza il ";" finale. Le ultime righe corrispondono alla sintassi di gnuplot per salvare il grafico come un file postscript di nome eq_diff.ps (octave usa gnuplot per la generazione del grafico).
Le funzioni richiamabili con octave sono disponibili anche sotto forma di libreria. Questo consente di "linkarle" eventualmente a un nostro programma, includendo nel sorgente l'header file dove si trovano i prototipi e la definizione delle costanti tramite la dichiarazione:
#include <octave/oct.h> |
maxima (http://maxima.sourceforge.net/) [8] è un programma per la manipolazione di espressioni simboliche, con le quali è possibile realizzare una gran quantità di operazioni diverse. È scritto in lisp e ha una storia molto lunga, che parte sin dagli anni '70. In questo primo periodo, il software, che si chiamava macsyma, aveva una licenza molto restrittiva. Poi, W. Schelter riuscì a ottenere il permesso per rilasciarlo sotto licenza GPL. Il programma è molto potente ed è così completo che il team di sviluppo (molto attivo) non ha come priorità l'implementazione di più funzionalità, ma piuttosto quella di correggere bug e redigere documentazione. Questo fatto parla da solo sulla qualità del software.
Le aree di utilizzo, a grandi linee, sono queste:
| Semplificazione di espressioni | Interpolazione |
| Rappresentazione grafica bi e tridimensionale | Statistica |
| Polinomi | Matrici e algebra lineare |
| Trigonometria | Calcolo tensoriale |
| Funzioni speciali | Serie |
| Limiti | Teoria di numeri |
| Differenziazione | Simmetrie |
| Integrazione | Teoria di gruppi |
| Risoluzione di equazioni |
Inoltre, maxima dispone di una serie di parole chiave che permettono di modificare il flusso del programma, con le quali è possibile costruire script per realizzare operazioni complesse. Vediamo adesso alcuni esempi di utilizzo.
Con octave abbiamo calcolato la moltiplicazione di due matrici: la matrice A di ordine 2 x 3 e la matrice B di ordine 3 x 5 per dare una matrice 2 x 5. Immaginiamo uno studente di secondaria che sta cominciando ad avere a che fare con i rudimenti dell'algebra lineare e che non si ricorda come si fa a moltiplicare due matrici. In questa situazione maxima può essere di aiuto:
(C1) A:genmatrix(A,2,3);
[ A A A ]
[ 1, 1 1, 2 1, 3 ]
(D1) [ ]
[ A A A ]
[ 2, 1 2, 2 2, 3 ]
(C2) B:genmatrix(B,3,5);
[ B B B B B ]
[ 1, 1 1, 2 1, 3 1, 4 1, 5 ]
[ ]
(D2) [ B B B B B ]
[ 2, 1 2, 2 2, 3 2, 4 2, 5 ]
[ ]
[ B B B B B ]
[ 3, 1 3, 2 3, 3 3, 4 3, 5 ]
(C3) A . B;
[ A B + A B + A B ]
[ 1, 3 3, 1 1, 2 2, 1 1, 1 1, 1 ]
(D3) Col 1 = [ ]
[ A B + B A + B A ]
[ 2, 3 3, 1 2, 1 2, 2 1, 1 2, 1 ]
[ A B + A B + A B ]
[ 1, 3 3, 2 1, 2 2, 2 1, 1 1, 2 ]
Col 2 = [ ]
[ A B + A B + B A ]
[ 2, 3 3, 2 2, 2 2, 2 1, 2 2, 1 ]
[ A B + A B + A B ]
[ 1, 3 3, 3 1, 2 2, 3 1, 1 1, 3 ]
Col 3 = [ ]
[ A B + A B + B A ]
[ 2, 3 3, 3 2, 2 2, 3 1, 3 2, 1 ]
[ A B + A B + A B ]
[ 1, 3 3, 4 1, 2 2, 4 1, 1 1, 4 ]
Col 4 = [ ]
[ A B + A B + B A ]
[ 2, 3 3, 4 2, 2 2, 4 1, 4 2, 1 ]
[ A B + A B + A B ]
[ 1, 3 3, 5 1, 2 2, 5 1, 1 1, 5 ]
Col 5 = [ ]
[ A B + A B + B A ]
[ 2, 3 3, 5 2, 2 2, 5 1, 5 2, 1 ] |
Gli input dati al programma hanno un numero progressivo con la lettera C iniziale; l'output ha invece una D iniziale. La funzione genmatrix() serve a generare le matrici per l'esempio, dopoché viene realizzata la moltiplicazione (A . B nella sintassi di maxima). Il risultato finale (D3) è praticamente una definizione del prodotto tra matrici.
Vediamo un esempio un po' più complesso: il calcolo di un integrale doppio. Supponiamo di voler calcolare il seguente integrale indefinito:
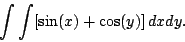
maxima ci dà il seguente risultato:
(C1) expr:sin(x) + cos(y); (D1) COS(y) + SIN(x) (C2) integrate(integrate(expr, x), y); (D2) x SIN(y) - COS(x) y |
Cioè:
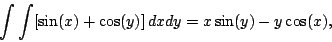
che è corretto. Come si vede, si istruisce il programma di integrare prima sulla variabile x, e il risultato sulla variabile y. Andiamo un po' oltre, calcoliamo l'integrale definito:
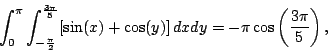
(C1) expr:sin(x) + cos(y);
(D1) COS(y) + SIN(x)
(C2) integrate(integrate(expr, x, -%pi / 2, 3 * %pi / 5), y, 0, %pi);
3 %PI
(D2) - %PI COS(-----)
5
(C3) float(%);
(D3) 0.97080551936273 |
float(%) significa "il risultato numerico dell'espressione precedente"; %pi rappresenta il valore del numero π.
L'integrale calcolato ha esistenza e quindi l'integrazione simbolica è fattibile. Alcune funzioni non sono però integrabili, e per calcolarle bisogna realizzare un'approssimazione alla funzione, ad esempio con uno sviluppo in serie di Taylor:
(C1) expr:sin(x) + cos(y);
(D1) COS(y) + SIN(x)
(C2) tay:taylor(expr, [x, 0, 20], [y, 0, 20]);
2 4 6 8 10 12 14
y y y y y y y
(D2)/T/ 1 - -- + -- - --- + ----- - ------- + --------- - -----------
2 24 720 40320 3628800 479001600 87178291200
16 18 20
y y y
+ -------------- - ---------------- + ------------------- + . . . + x
20922789888000 6402373705728000 2432902008176640000
3 5 7 9 11 13 15
x x x x x x x
- -- + --- - ---- + ------ - -------- + ---------- - -------------
6 120 5040 362880 39916800 6227020800 1307674368000
17 19
x x
+ --------------- - ------------------ + . . .
355687428096000 121645100408832000
(C3) float(integrate(integrate(tay, x, -%pi / 2, 3 * %pi / 5), y, 0, %pi));
(D3) 0.97080551939849 |
Lo sviluppo in serie di Taylor è un modo per approssimare una funzione qualsiasi con precisione arbitraria a partire dai valori della funzione e delle sue derivate. Il risultato è una somma delle potenze delle variabili indipendenti, troncata a un ordine stabilito, che dà un'approssimazione alla funzione di partenza; più termini si prendono e più accurato sarà il risultato finale. L'esempio è particolarmente istruttivo, perché realizza lo sviluppo in serie di una funzione di due variabili. Lo sviluppo viene fatto intorno al punto zero e si prendono le prime 20 potenze per ogni variabile (x e y). Il risultato mostra che effettivamente lo sviluppo in serie rappresenta una buona approssimazione della funzione, essendo il risultato del calcolo dell'integrale molto vicino al valore vero di 0.97080551936273.
Queste esempi sono sufficienti per avere un'idea delle potenzialità del programma. Per ulteriori approfondimenti si rimanda alla documentazione riportata in bibliografia [8].
In questa seconda parte abbiamo illustrato sommariamente certe caratteristiche interessanti di alcuni software importanti. L'obiettivo che ci eravamo prefissati era quello di dare una idea, con l'aiuto di alcuni esempi, delle loro potenzialità. Spero che quanto detto abbia stuzzicato qualcuno ad approfondire alcuni degli argomenti trattati.
La Parte III sarà interamente dedicata all'interfacciamento grafico. Faremo alcune considerazioni di carattere generale, per poi presentare un'applicazione web che implementa un interfacciamento a maxima per la risoluzione simbolica e la rappresentazione grafica di integrali multidimensionali.
1)
Kris Buytaert.
The openMosix HOWTO, Revision v1.0.3, june 2004.
2)
John W. Eaton.
Gnu Octave, A high-Level Interactive Language for Numerical
Computations, third edition, February 1997.
http://www.octave.org.
3)
Mark Galassi, Jim Davies, James Theiler, Crian Gough, Gerard Jungman, Michael
Booth, and Fabrice Rossi.
Gnu Scientific Library, Reference Manual.
Network Theory Limited, Bristol, UK, 1.3 edition, February 2003.
4)
Al Geist, Adam Beguelin, Jack Dongarra, Weicheng Jiang, Robert Manchek, and
Vaidy Sunderam.
PVM3 User's Guide and Reference Manual.
Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, September 1994.
5)
David Kotz.
Latex and the gnuplot plotting program, July 1991.
6)
Andy Liaw and Dick Crawford.
Gnuplot 3.5, user's guide, 1994.
7)
Philip A. Nelson.
bc, an arbitrary precision calculator language.
Free Software Foundation, Boston, MA, USA, 1997.
Version 1.06.
8)
William F. Schelter.
Maxima, versione 5.4.
http://www.ma.utexas.edu/maxima.html.
9)
Thomas Williams and Colin Kelley.
Gnuplot, An Interactive Plotting Program, October 2000.
Version 3.7.
10)
Thomas Williams and Colin Kelley.
Gnuplot, An Interactive Plotting Program, April 2004.
Version 4.0.
L'autoreFrancisco Yepes Barrera, Paco, è socio di ILS ed appassionato per diletto e per lavoro di informatica e di scienze. I suoi interessi riguardano la computazione scientifica, l'intelligenza artificiale e l'utilizzo di software libero nella soluzione di problemi matematici. |
|
<- User-Mode Linux - Indice Generale - Copertina - Una risposta a Nikolai Bezroukov -> |

|